2D Robot Localization - Tutorial

This tutorial introduces the main aspects of UKF-M.

Goals of this script:

• understand the main principles of Unscented Kalman Filtering on Manifolds (UKF-M) [BBB19].

• get familiar with the implementation.

• design an UKF for a vanilla 2D robot localization problem.

We assume the reader to have sufficient prior knowledge with (unscented) Kalman filtering. However, we require really approximate prior knowledge and intuition about manifolds and tangent spaces.

This tutorial describes all one require to design an Unscented Kalman Filter (UKF) on a (parallelizable) manifold, and puts in evidence the versatility and simplicity of the method in term of implementation. Indeed, we need to define an UKF on parallelizable manifolds:

1. a model of the state-space system that specifies the propagation and measurement functions of the system.

2. an uncertainty representation of the estimated state, which is a mapping that generalizes the linear uncertainty definition \(\mathbf{e} = \mathbf{x} - \mathbf{\hat{x}}\).

3. standard UKF parameters that are noise covariance matrices and sigma point parameters.

We introduce the methodology by addressing the vanilla problem of robot localization, where the robot obtains velocity measurements, e.g., from wheel odometry, and position measurements, e.g., from GPS. The state consists of the robot orientation along with the 2D robot position. We reproduce the example described in [BB17], Section IV.

Import

Package import is minimal, as UKF-M is mainly build on the standard NumPy package.

import ukfm
import numpy as np
import matplotlib
ukfm.utils.set_matplotlib_config()
# The matplotlib configuration is adjusted for better rendering the figures.

The Model

The first ingredient we need is a model that defines:

1. the state of the system at instant \(n\), noted \(\boldsymbol{\chi}_n \in \mathcal{M}\), where \(\mathcal{M}\) is a parallelizable manifold (vectors spaces, Lie groups and others). Here the state corresponds to the robot orientation and the robot position:

   \[\mathcal{M} = \left\{ \begin{matrix} \mathbf{C} \in SO(2), \mathbf{p} \in \mathbb R^2 \end{matrix} \right\}.\]

2. a propagation function that describes how the state evolves along time

   \[\boldsymbol{\chi}_n = f(\boldsymbol{\chi}_{n-1}, \boldsymbol{\omega}_{n}, \mathbf{w}_{n}) \in \mathcal{M},\]

   where \(\boldsymbol{\omega}_{n} \in \mathcal{U}\) is the input of the system and \(\mathbf{w}_{n} \sim \mathcal{N}(\mathbf{0}, \mathbf{Q}_n)\) is a Gaussian noise.

3. an observation function describing the measures we have in the form of:

   \[\mathbf{y}_n = h(\boldsymbol{\chi}_{n}) + \mathbf{v}_n \in \mathbb{R}^p,\]

   where \(\mathbf{v}_{n} \sim \mathcal{N}(\mathbf{0}, \mathbf{R}_n)\) is a Gaussian noise.

The code contains models, which are declared as class. In this script, we use the LOCALIZATION model.

MODEL = ukfm.LOCALIZATION

Note

A state or an input is an instance of the STATE or INPUT class that is described in the MODEL, and can thus handle a complex form not restricted to vector. In contrast, we consider for conciseness that any measurement at time \(n\) is a vector (1D-array).

Simulating the Model

We compute simulated data, where the robot drives along a 10 m diameter circle for 40 seconds with high rate odometer measurements (100 Hz) and low rate position measurements (1 Hz). We first define the model parameters, create an instance of the model, and compute the true states along with noisy inputs.

# sequence time (s)
T = 40
# odometry frequency (Hz)
odo_freq = 100
#  create the model
model = MODEL(T, odo_freq)
# odometry noise standard deviation
odo_std = np.array([0.01,          # longitudinal speed (v/m)
                    0.01,          # transverse shift speed (v/m)
                    1/180*np.pi])  # differential odometry (rad/s)
# radius of the circle trajectory (m)
radius = 5
# simulate trajectory
states, omegas = model.simu_f(odo_std, radius)

Note

The model encodes how non-linear noise affects the propagation function. In contrast, we assume measurement noise affects the observations linearly. It spares us computational time, but the method can be adapted to handle non-linear observation noises of the form \(\mathbf{y}_n = h(\boldsymbol{\chi}_{n}, \mathbf{v}_n)\).

The state and input variables are both a list of STATE and INPUT instances. One can access a variable at specific instant \(n\) as:

state_n = states[n] # model.STATE instance
omega_n = omegas[n] # model.INPUT instance

We can access to the elements of the state or the input as:

state_n.Rot    # 2d orientation encoded in a rotation matrix
state_n.p      # 2d position
omega_n.v      # robot forward velocity
omega_n.gyro   # robot angular velocity

These elements depend on the considered problem and are defined in the model. See at the LOCALIZATION() documentation to get a brief mathematical description.

Note

The orientation states[n].Rot is defined via a rotation matrix. We always define for clarity orientations in matrices living in \(SO(2)\) and \(SO(3)\). The method remains compatible with quaternion. We may drop some numerical issues, e.g. round-off that leads to non-orthogonal rotation matrices, to let the code simple.

With the true states, we simulate noisy measurements.

# GPS frequency (Hz)
gps_freq = 1
# GPS noise standard deviation (m)
gps_std = 1
# simulate measurements
ys, one_hot_ys = model.simu_h(states, gps_freq, gps_std)

The variable ys is a 2D array that contains all the observations of the sequence. To get the k-th measurement, take the k-th element of the variable as:

y_k = ys[k] # vector (1D array)

We have defined an array one_hot_ys that contains 1 at instant where a measurement happens and 0 otherwise.

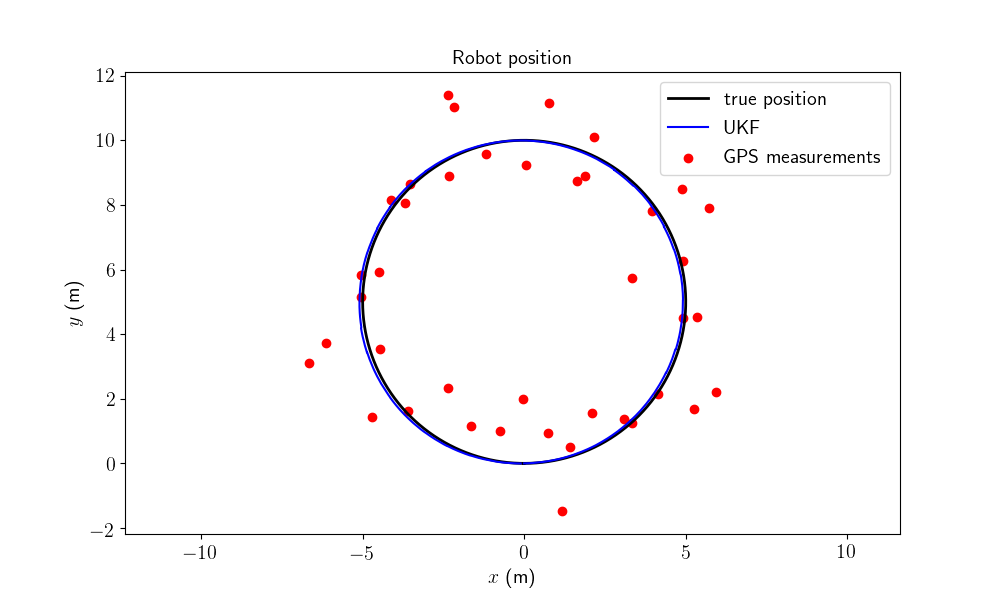
Let us visualizes the robot trajectory along with measurements.

model.plot_traj(states, ys)

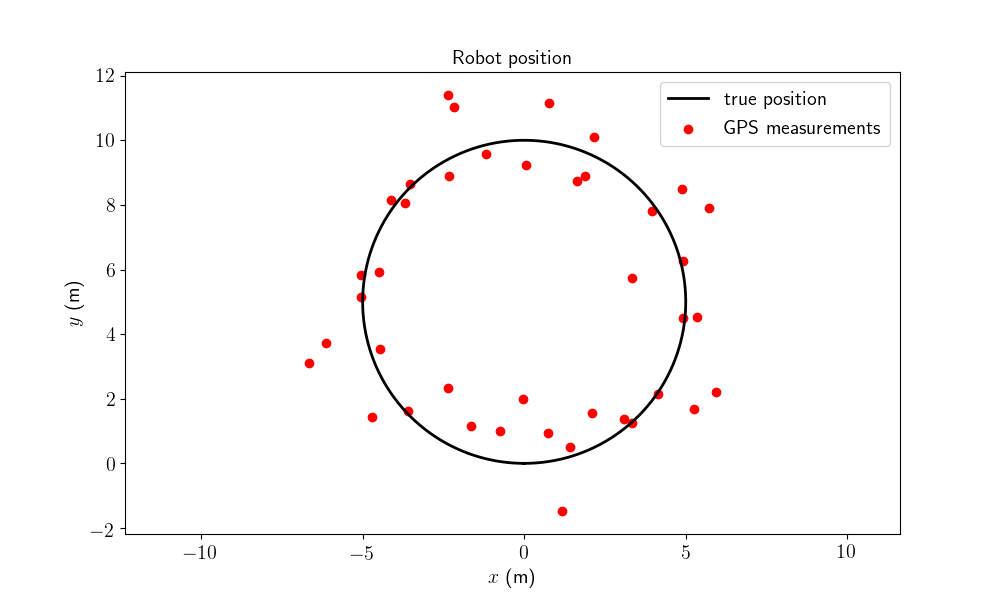
GPS measurements are visibly noisy.

Filter Design

Designing an UKF on parallelizable manifolds consists in:

1. defining a model of the propagation function and the measurement function.

2. choosing the retraction \(\varphi(.,.)\) and inverse retraction \(\varphi^{-1}_.(.)\) such that

   \[ \begin{align}\begin{aligned}\boldsymbol{\chi} &= \varphi(\hat{\boldsymbol{\chi}}, \boldsymbol{\xi}) \in \mathcal{M},\\\boldsymbol{\xi} &= \varphi^{-1}_{\hat{\boldsymbol{\chi}}} (\boldsymbol{\chi}) \in \mathbb{R}^d,\end{aligned}\end{align} \]

   where \(\boldsymbol{\chi}\) is the true state, \(\hat{\boldsymbol{\chi}}\) the estimated state, and \(\boldsymbol{\xi}\) the state uncertainty (we does not use the notation \(\mathbf{x}\) and \(\mathbf{e}\) to emphasize the differences with the linear case).

3. setting UKF parameters such as sigma point dispersion and noise covariance values.

Step 1) is already done, as we take the functions defined in the model.

Step 2) consists in choosing the mapping that encode our representation of the state belief. A basic UKF is building on the uncertainty defined as \(\mathbf{e} = \mathbf{x} - \mathbf{\hat{x}}\), which is not necessary optimal. Rather than, we define the uncertainty \(\boldsymbol{\xi}\) thought \(\boldsymbol{\chi} = \varphi(\hat{\boldsymbol{\chi}}, \boldsymbol{\xi})\), where the retraction \(\varphi(.,.)\) has to satisfy \(\varphi(\boldsymbol{\chi}, \mathbf{0}) = \boldsymbol{\chi}\) (without uncertainty, the estimated state equals the true state). We then need an inverse retraction to get a difference from two states that must respect \(\varphi^{-1}_{\boldsymbol{\chi}}(\boldsymbol{\chi}) = \mathbf{0}\).

We embed here the state in \(SO(2) \times \mathbb{R}^2\), such that:

• the retraction \(\varphi(.,.)\) is the \(SO(2)\) exponential for orientation and the vector addition for position.

• the inverse retraction \(\varphi^{-1}_.(.)\) is the \(SO(2)\) logarithm for orientation and the vector subtraction for position.

Note

We define different choices of retraction and inverse retraction directly in the model.

Note

One can suggest alternative retractions, e.g. by viewing the state as a element of \(SE(2)\). In the benchmarks section, we compare different choices of retraction for different problems.

We define the filter parameters based on the model.

# propagation noise covariance matrix
Q = np.diag(odo_std ** 2)
# measurement noise covariance matrix
R = gps_std ** 2 * np.eye(2)
# sigma point parameters
alpha = np.array([1e-3, 1e-3, 1e-3])
# this parameter scales the sigma points.
# Current values are between 10^-3 and 1.

Filter Initialization

We initialize the filter with the true state with a small heading error of 1°.

# "add" orientation error to the initial state
state0 = model.STATE(Rot=states[0].Rot.dot(ukfm.SO2.exp(1/180*np.pi)),
                     p=states[0].p)
# initial state uncertainty covariance matrix
P0 = np.zeros((3, 3))
# The state is not perfectly initialized
P0[0, 0] = (1/180*np.pi)**2

We define the filter as an instance of the UKF class.

ukf = ukfm.UKF(state0=state0,          #  initial state
               P0=P0,                  # initial covariance
               f=model.f,              # propagation model
               h=model.h,              # observation model
               Q=Q,                    # process noise covariance
               R=R,                    # observation noise covariance
               phi=model.phi,          # retraction
               phi_inv=model.phi_inv,  # inverse retraction
               alpha=alpha             # sigma point parameters
               )

Before launching the filter, we set a list for recording estimates along the full trajectory and a 3D array to record covariance estimates.

ukf_states = [ukf.state]
ukf_Ps = np.zeros((model.N, 3, 3))
ukf_Ps[0] = ukf.P

Filtering

The UKF proceeds as a standard Kalman filter with a for loop.

# measurement iteration number (first measurement is for n == 0)
k = 1
for n in range(1, model.N):
    # propagation
    ukf.propagation(omegas[n-1], model.dt)
    # update only if a measurement is received
    if one_hot_ys[n] == 1:
        ukf.update(ys[k])
        k += 1
    # save estimates
    ukf_states.append(ukf.state)
    ukf_Ps[n] = ukf.P

Results

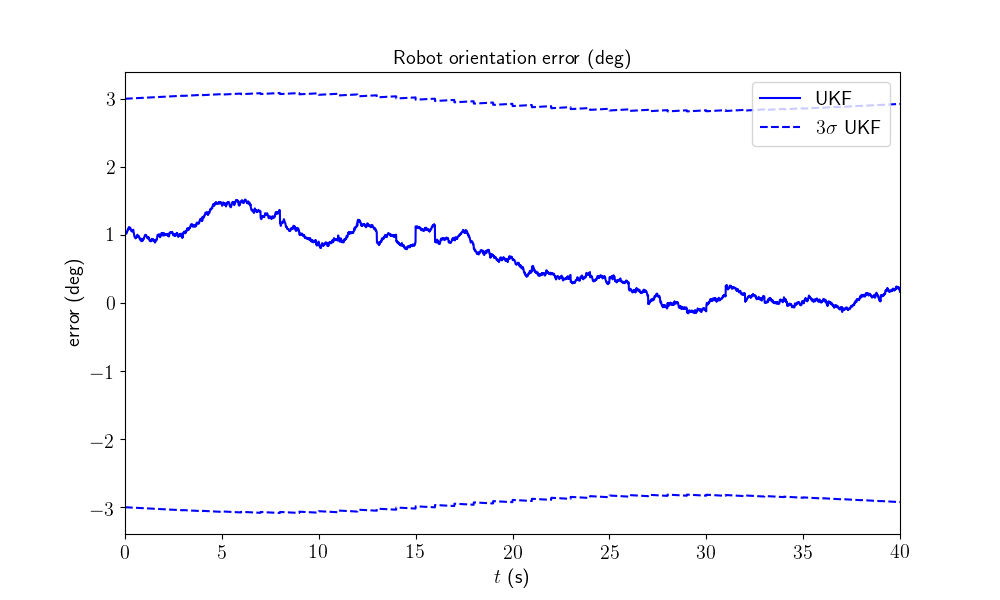
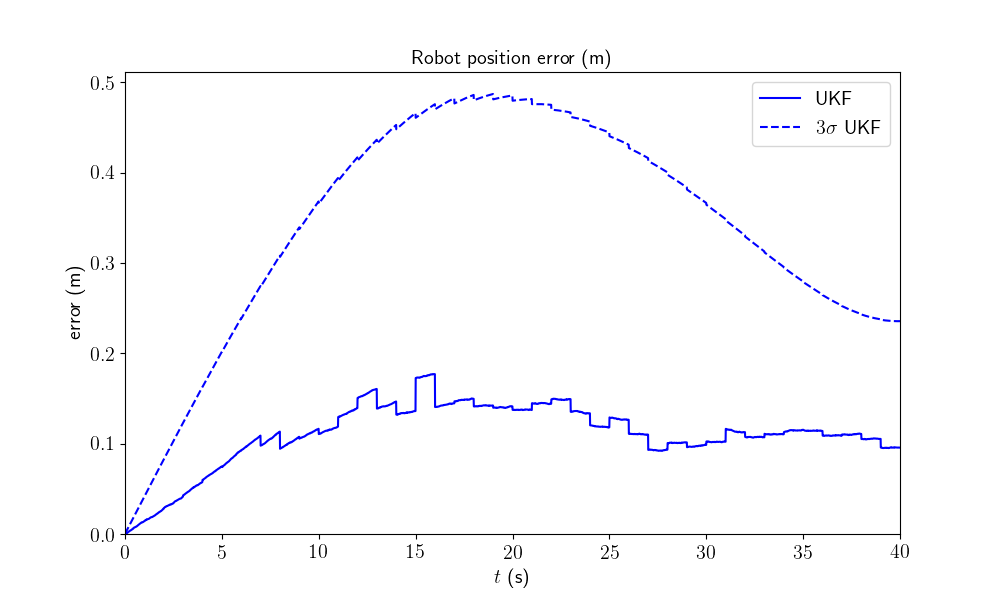
We plot the trajectory, GPS measurements and estimated trajectory. We then plot the orientation and position errors along with 95% (\(3\sigma\)) confident interval. The results has to be confirmed with average metrics to reveal the filter performances in term of accuracy, consistency and robustness.

model.plot_results(ukf_states, ukf_Ps, states, ys)

• 
• 
• 

All results seem coherent. This is expected as the initial heading error is small.

Conclusion

This script introduces UKF-M and shows how designing an UKF on parallelizable manifolds mainly consists in choosing an advantageous uncertainty representation. Two major interests of the method are that many problems could be addressed within the framework, and that both the theory and its implementation are sufficiently simple.

The filter works apparently well on a simple robot localization problem, with small initial heading error. Is it hold for more challenging initial error ?

You can now:

• enter more in depth with the theory, see [BBB19].

• address the UKF for the same problem with different noise parameters, and test its robustness to strong initial heading error.

• modify the propagation model with a differential odometry model, where inputs are left and right wheel speed measurements.

• apply the UKF for the same problem on real data.

• benchmark the UKF with different retractions and compare the new filters to both the extended Kalman filter and invariant extended Kalman filter of [BB17].