Attitude Estimation with an IMU - Example

Goal of this script:

• applying the UKF for estimating 3D attitude from an IMU.

We assume the reader is already familiar with the tutorial.

Attitude estimation with an Inertial Measurement Unit (IMU). The filter fuses measurements coming from gyros, accelerometers and magnetometers. The IMU does not have any bias. We reproduce the simulation based on [KHSchon17].

Import

from scipy.linalg import block_diag
from ukfm import ATTITUDE as MODEL
import ukfm
import numpy as np
import matplotlib
ukfm.utils.set_matplotlib_config()

Model and Simulation

This script uses the ATTITUDE() model that requires the sequence time and the IMU frequency.

# sequence time (s)
T = 100
# IMU frequency (Hz)
imu_freq = 100
# create the model
model = MODEL(T, imu_freq)

The true trajectory is computed along with noisy inputs after we define the noise standard deviation affecting the IMU, where the platform is 2 s stationary and then has constant angular velocity around gravity.

# IMU noise standard deviation (noise is isotropic)
imu_std = np.array([5/180*np.pi,  # gyro (rad/s)
                    0.4,          # accelerometer (m/s^2)
                    0.2])         # magnetometer
# simulate true trajectory and noisy inputs
states, omegas = model.simu_f(imu_std)

The state and the input contain the following variables:

states[n].Rot      # 3d orientation (matrix)
omegas[n].gyro     # robot angular velocities

We compute noisy measurements based on the true states.

ys = model.simu_h(states, imu_std)

A measurement ys[k] contains accelerometer and magnetometer measurements.

Filter Design and Initialization

We embed the state in \(SO(3)\) with left multiplication, such that:

• the retraction \(\varphi(.,.)\) is the \(SO(3)\) exponential where the state multiplies the uncertainty on the left.

• the inverse retraction \(\varphi^{-1}_.(.)\) is the \(SO(3)\) logarithm.

# propagation noise covariance matrix
Q = imu_std[0]**2*np.eye(3)
# measurement noise covariance matrix
R = block_diag(imu_std[1]**2*np.eye(3), imu_std[2]**2*np.eye(3))
# initial uncertainty matrix
P0 = np.zeros((3, 3))  # The state is perfectly initialized
# sigma point parameters
alpha = np.array([1e-3, 1e-3, 1e-3])

We initialize the filter with the true state.

state0 = model.STATE(Rot=states[0].Rot)
ukf = ukfm.UKF(state0=state0,
               P0=P0,
               f=model.f,
               h=model.h,
               Q=Q,
               R=R,
               phi=model.phi,
               phi_inv=model.phi_inv,
               alpha=alpha)
# set variables for recording estimates along the full trajectory
ukf_states = [state0]
ukf_Ps = np.zeros((model.N, 3, 3))
ukf_Ps[0] = P0

Filtering

The UKF proceeds as a standard Kalman filter with a for loop.

for n in range(1, model.N):
    # propagation
    ukf.propagation(omegas[n-1], model.dt)
    # update
    ukf.update(ys[n])
    # save estimates
    ukf_states.append(ukf.state)
    ukf_Ps[n] = ukf.P

Results

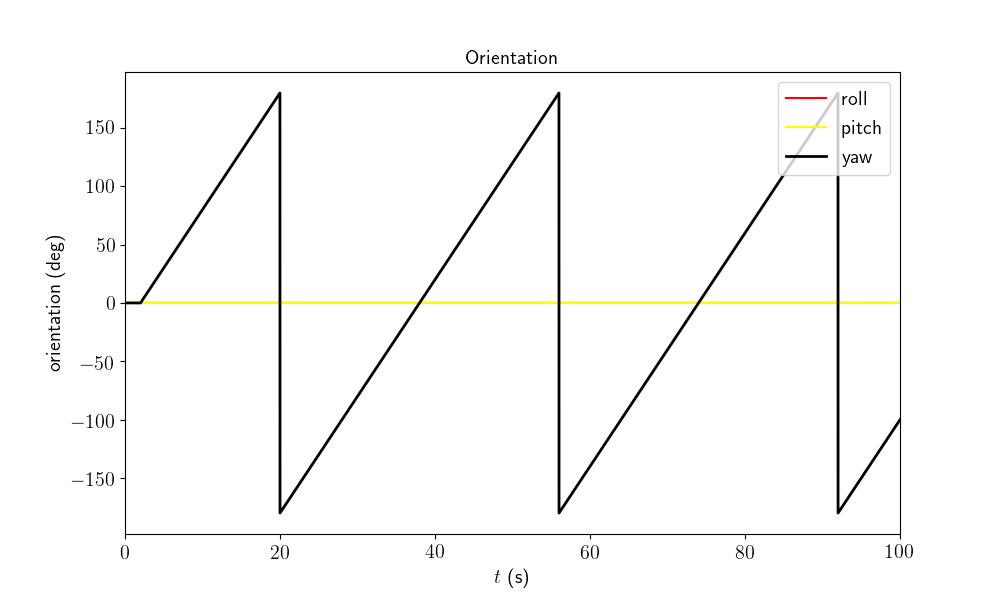
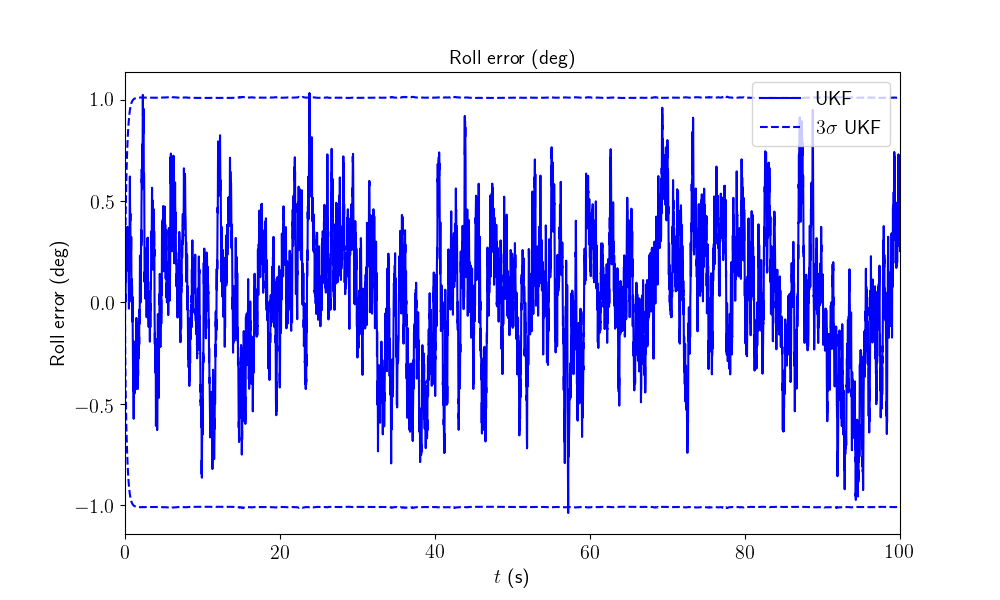
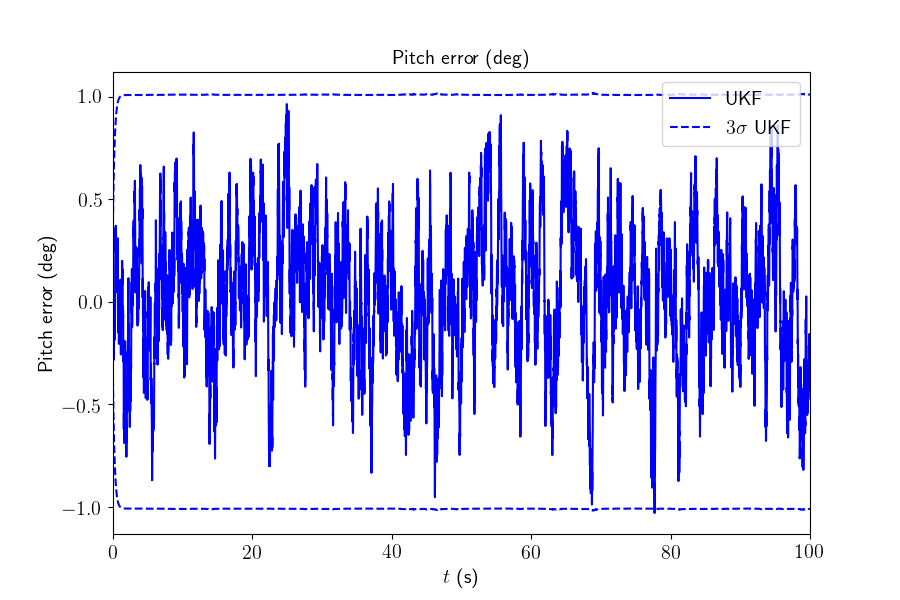
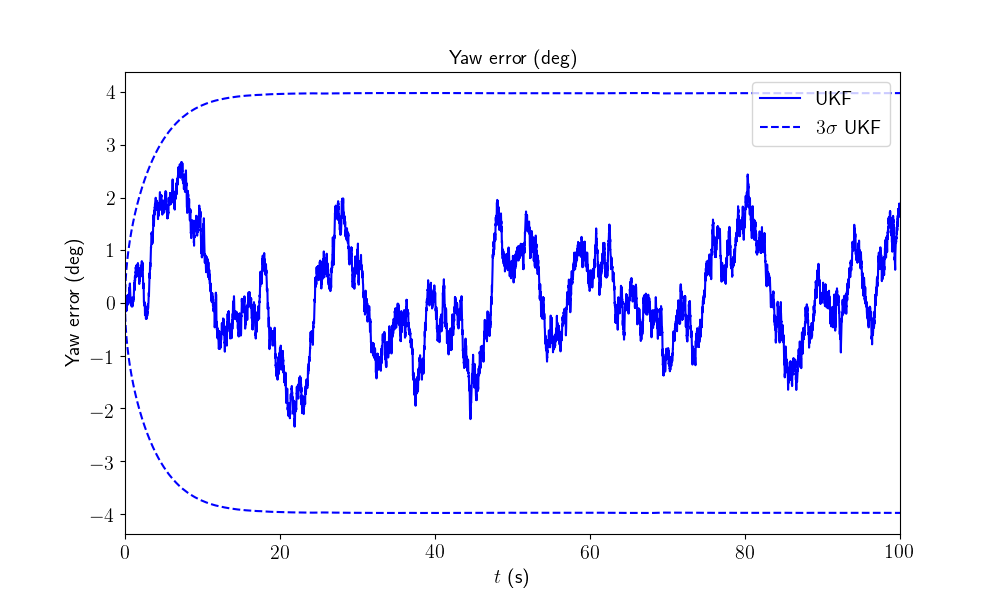
We plot the orientation as function of time and the orientation error.

model.plot_results(ukf_states, ukf_Ps, states, omegas)

• 
• 
• 
• 

The trajectory starts by a small stationary step following by constantly turning around the gravity vector (only the yaw is increasing).

We have plotted the 95% (\(3\sigma\)) confident interval and see the error is mainly below behind this interval: in this situation the filter covariance output matches especially well the error behavior.

Conclusion

This script shows how well works the UKF on parallelizable manifolds for estimating the orientation of a platform from an IMU.

You can now:

• address the UKF for the same problem with different noise parameters.

• add outliers in acceleration or magnetometer measurements.

• benchmark the UKF with different retractions and compare it to the extended Kalman filter in the Benchmarks section.