2D Robot SLAM - Example
Goals of this script:
- apply the UKF for performing 2D SLAM (Simultaneous Localization And Mapping).
- discover a computationally alternative way for performing UKF insipred from [HMR13]. This alternative leads to computational speed improvement when only a part of the state is involved in a propagation or in update step.
- augment the state when a new landmark is observed in a UKF derivative-free way.
We assume the reader is already familiar with the approach described in the tutorial.
This script considers the 2D robot SLAM problem where the robot is equipped with wheel odometry and observes unknown landmark measurements. The robot state is propagated through the odometry model and landmark observations are used in the UKF measurement step. Landmarks are static and we assume no error coming from data association. We reproduce the simulations that are described in [HMR10], [HMR13].
Contents
Initialization
Start by cleaning the workspace.
clear all; close all;
Simulation
The trajectory of the robot consists of turning at constant speed.
% sequence time (s) T = 2500; % odometry frequency (Hz) odo_freq = 1; % true speed of robot (m/s) v = 0.25; % true angular velocity (rad/s) gyro = 1.5/180*pi; % odometry noise standard deviation (see [1]) odo_noise_std = [0.05*v/sqrt(2); % speed (v/m) 0.05*v*sqrt(2)*2]; % angular speed (rad/s) % observation noise standard deviation (m) obs_noise_std = 0.1; % total number of timestamps N = T*odo_freq; % integration step (s) dt = 1/odo_freq;
When simulating data, we generate a map. The map consists of landmarks constantly spaced on a circle with slightly higher radius than the radius of the robot trajectory.
% simulate true trajectory and noisy input [states, omegas, ldks] = slam2d_simu_f(T, odo_freq, odo_noise_std, v, gyro); % number of landmarks N_ldk = size(ldks, 2);
The state and the input contain the following variables:
states(n).Rot % orientation (matrix) states(n).p % robot position states(n).p_l % landmark positions omegas(n).gyro % robot angular velocity omegas(n).v % robot speed
We compute noisy landmark measurements based on the true states.
% simulate landmark measurements
ys = slam2d_simu_h(states, obs_noise_std, N_ldk, ldks);
A measurement contains observation of all visible landmarks as:
y = ys(:, :, n) % measurement at timestamp n y_k = n(:, k) % k-th observed landmark at instant n, where y_k(3) % is the landmark indice
Filter Design and Initialization
We choose to embed the robot state in 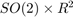 and each landmark position in
and each landmark position in 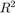 , such that:
, such that:
- the retraction
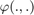 is the
is the 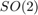 exponential for orientation, i.e. and the vector addition for robot and landmark positions.
exponential for orientation, i.e. and the vector addition for robot and landmark positions. - the inverse retraction
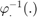 is the
is the 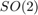 logarithm for orientation and the vector subtraction for robot and landmark positions.
logarithm for orientation and the vector subtraction for robot and landmark positions.
% propagation noise covariance matrix Q = diag(odo_noise_std.^2); % measurement noise covariance matrix R = obs_noise_std.^2 * eye(2); % initial uncertainty matrix P0 = zeros(3, 3); % The state is perfectly initialized without landmark % sigma point parameters alpha = [1e-3, 1e-3, 1e-3];
Regarding implementation, we use the Jacobian UKF (JUKF) that spares time when only a part of the space is involved in a propagation or update step.
% define UKF functions f = @slam2d_f; h = @slam2d_h; % reduced retraction used during propagation red_phi = @slam2d_red_phi; red_phi_inv = @slam2d_red_phi_inv; % retraction used during update up_phi = @slam2d_phi; % we do not need phi_inv fonction for update % retraction used for augmenting state z_aug = @slam2d_z_aug; aug_phi = @slam2d_aug_phi; aug_phi_inv = @slam2d_aug_phi_inv; % reduced weights during propagation red_weights = ukf_set_weight(3, 2, alpha); red_idxs = 1:3; % indices corresponding to the robot state in P % weights during update weights = ukf_set_weight(5, 2, alpha); aug_weights = ukf_set_weight(3, 2, alpha); aug_idxs = 1:3; % indices corresponding to the robot state in P cholQ = chol(Q); % initialize the filter ukf_state = states(1); ukf_state.p_l = []; ukf_P = P0; % set variables for recording estimates along the full trajectory ukf_states = ukf_state; ukf_Ps = zeros(N, length(ukf_P), length(ukf_P)); ukf_Ps(1, 1:length(ukf_P), 1:length(ukf_P)) = ukf_P; % indices of already observed landmarks ukf_lmk = [];
Filtering
The UKF proceeds as a standard Kalman filter with a for loop.
for n = 2:N % propagation [ukf_state, ukf_P] = ukf_jacobian_propagation(ukf_state, ukf_P, ... omegas(n-1), f, dt, red_phi, red_phi_inv, cholQ, red_weights, red_idxs); y = ys(:, :, n); N_y = length(find(y(3, :) > 0)); % set observalibity matrice and residual H = zeros(0, length(ukf_P)); res = zeros(0); % set ukf state for update ukf_up_state.Rot = ukf_state.Rot; ukf_up_state.p = ukf_state.p; Rot = ukf_state.Rot; p = ukf_state.p; % update each landmark already in the filter for i = 1:N_y idx = find(~(ukf_lmk - y(3, i))); if isempty(idx) continue end % indices of the robot and observed landmark in P up_idxs = [1:3 2+(2*idx:2*idx+1)]; ukf_up_state.p_l = ukf_state.p_l(:, idx); % compute observability matrices and residual [H_i, res_i] = ukf_jacobian_update(ukf_up_state, ukf_P, y(1:2, i), ... h, up_phi, weights, up_idxs); % increase observabily matrix and residual H = [H; H_i]; res = [res; res_i]; end % update only if some landmards have been observed if size(H, 1) > 0 R_n = obs_noise_std^2 * eye(size(H, 1)); % update state and covariance with Kalman update [ukf_state, ukf_P] = kf_update(ukf_state, ukf_P, H, res, R_n, up_phi); end % augment the state with new landmark for i = 1:N_y idx = find(~(ukf_lmk - y(3, i))); if ~isempty(idx) continue end % augment the landmark state ukf_lmk = [ukf_lmk; y(3, i)]; % indices of the new landmark idx = find(~(ukf_lmk - y(3, i))); up_idxs = [1:3 2+(2*idx:2*idx+1)]; % new landmark position p_l = p + Rot*y(1:2, i); ukf_up_state.p_l = p_l; ukf_state.p_l = [ukf_state.p_l p_l]; % get Jacobian and then covariance following [2] R_n = obs_noise_std^2 * eye(2); [~, ukf_P] = ukf_aug(ukf_state, ukf_P, y(1:2, i), z_aug, aug_phi, ... aug_phi_inv, aug_weights, aug_idxs, R_n); end % save estimates ukf_states(n) = ukf_state; ukf_Ps(n, 1:length(ukf_P), 1:length(ukf_P)) = ukf_P; end
Results
slam2d_results_plot(ukf_states, ukf_Ps, states, dt, ldks);
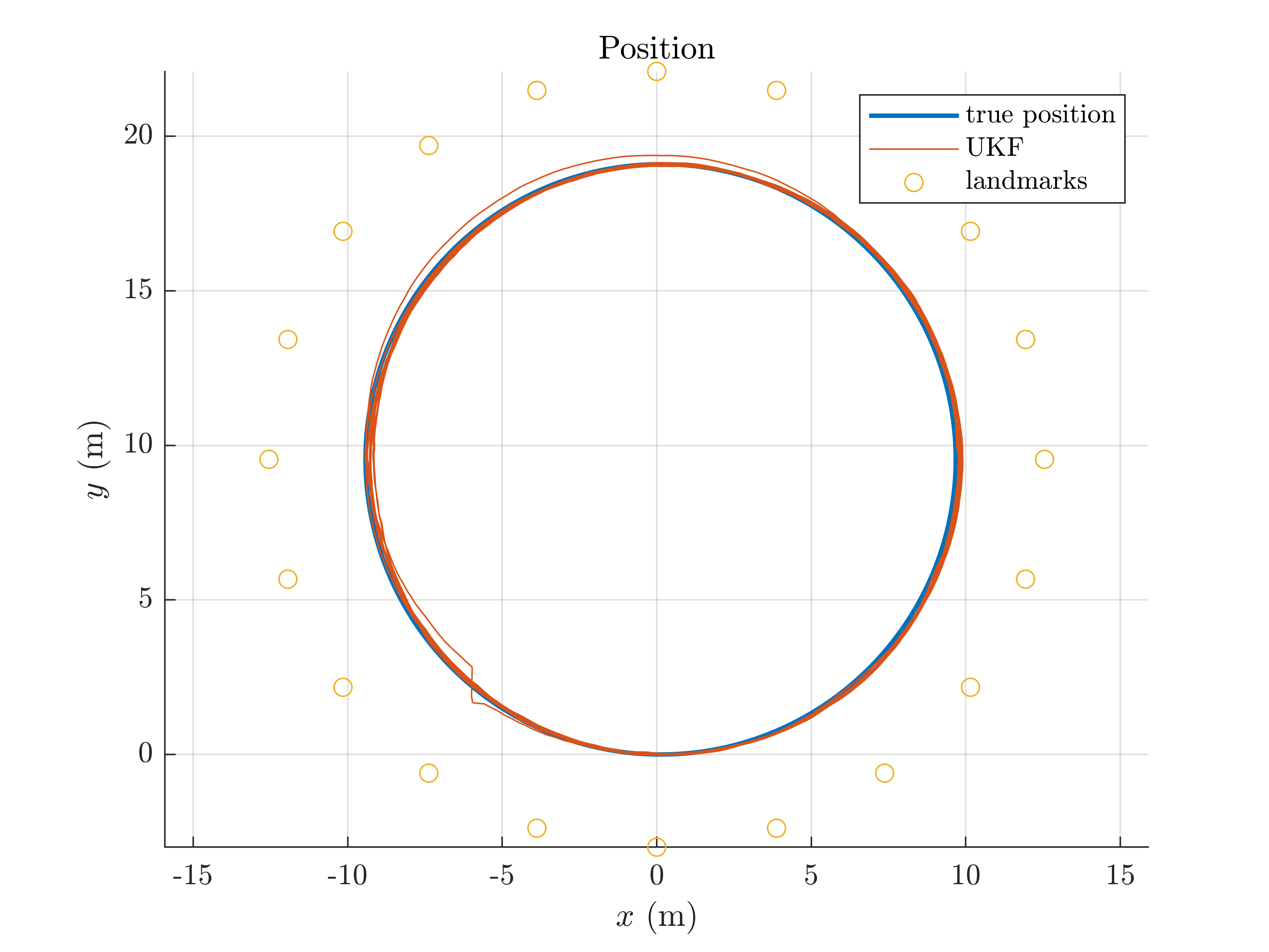
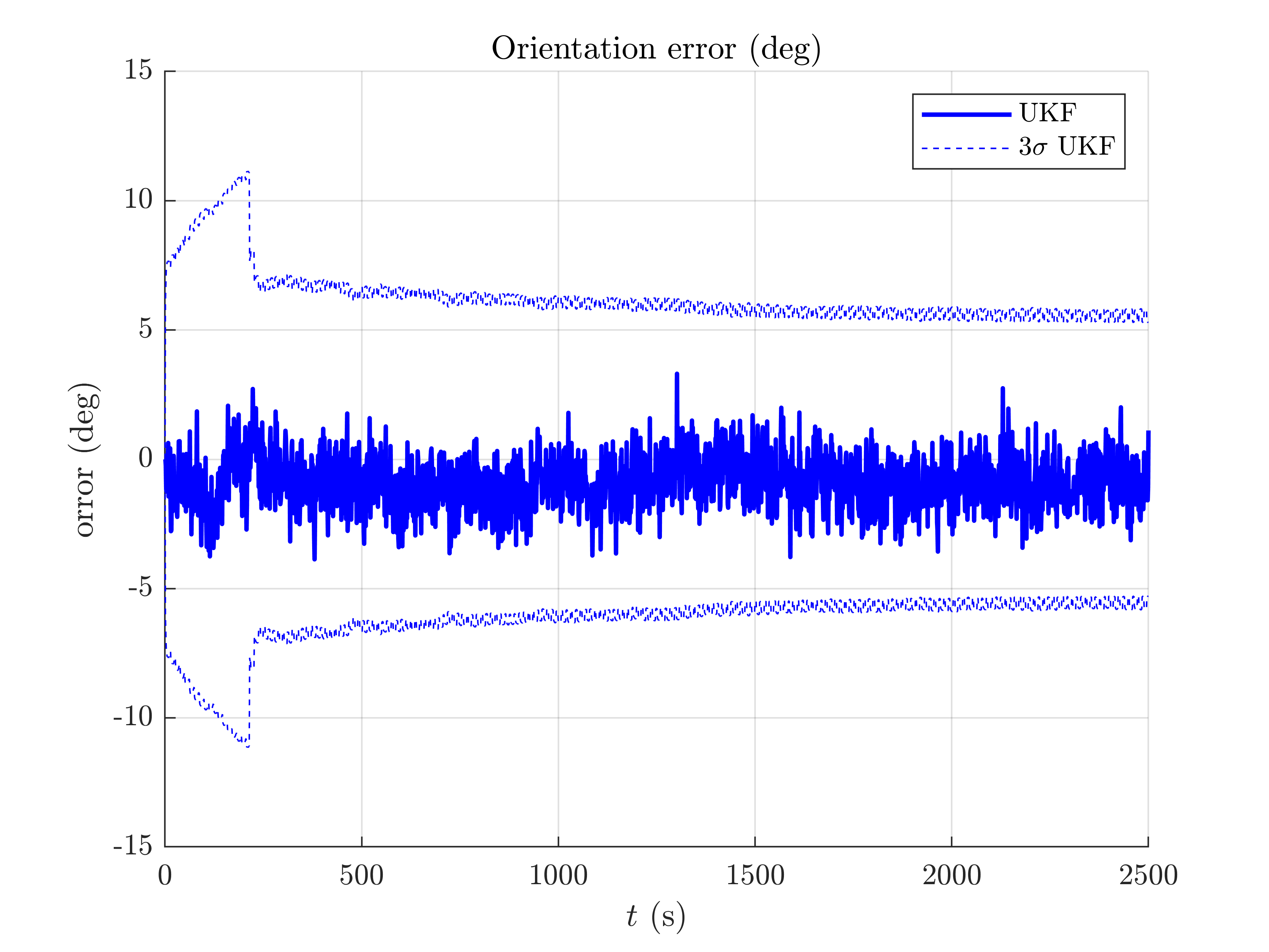
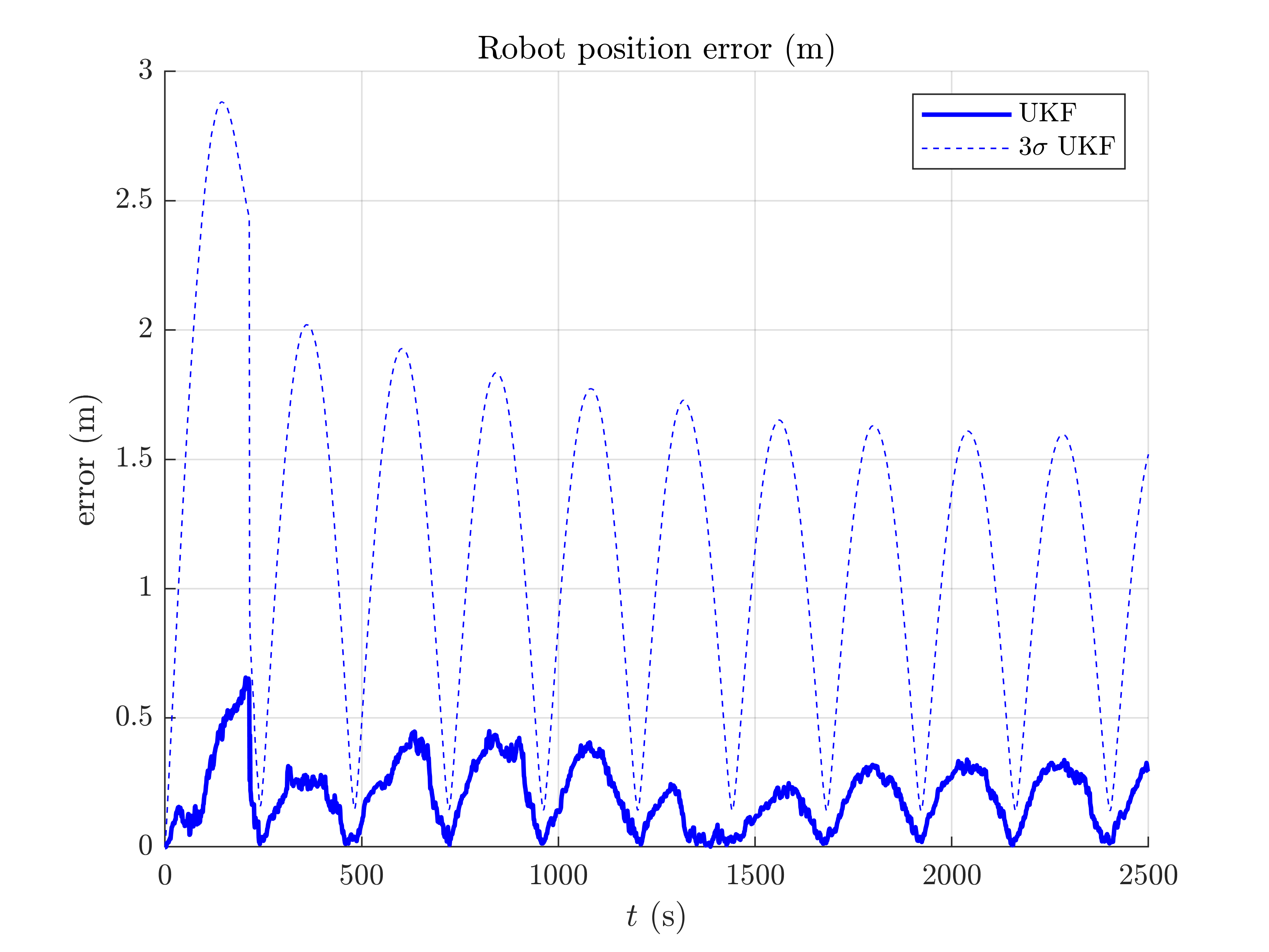
We note the  confidence interval decreases along time.
confidence interval decreases along time.
Conclusion
This script shows how the UKF on parallelizable manifolds can be used for 2D SLAM. By leveraging numerical Jacobian inference, one obtains a computationally more efficient filter. The UKF works for this example, but consistency issues happear at the end of the trajectory.
You can now:
- consider non-linear range and bearing measurement.
- benchmark the UKF with different retractions and compare it to the extended Kalman filter and the invariant extended Kalman filter of [BB17].